"Form follows function" said architect Louis Sullivan, arguing that
a building's purpose should determine its design. If Sullivan had
been a biologist he might have put it the other way around.
by Paul Preuss
Ever since James
Watson and Francis Crick solved the double helix structure of dna
in 1953, biology's most formidable structural challenge has been
the "protein folding problem" - learning how nature gets from a
gene, a length of dna that encodes the order of amino-acid residues
in a string, to a working protein, that same string intricately
folded into all the pockets and creases and knobs essential to the
physics and chemistry of life.
While protein
structures are being collected at a steadily increasing pace, knowledge
of gene sequences is exploding. The Human Genome Project, begun
by the Department of Energy and the National Institutes of Health
less than ten years ago, have finished a draft of all 50,000 to
100,000 human genes - all three billion base-pairs. The majority
of the proteins these myriad genes code for do not resemble any
already known.
"The more information
you have, the more kinds of information you need to make sense of
it," says Daniel Rokhsar, head of the Computational and Theoretical
Biology Department in the Lab's Physical Biosciences Division and
a professor of physics at the University of California at Berkeley.
"Without a simultaneous explosion in computation-powerful computers
and flexible programs-we'll be overwhelmed."
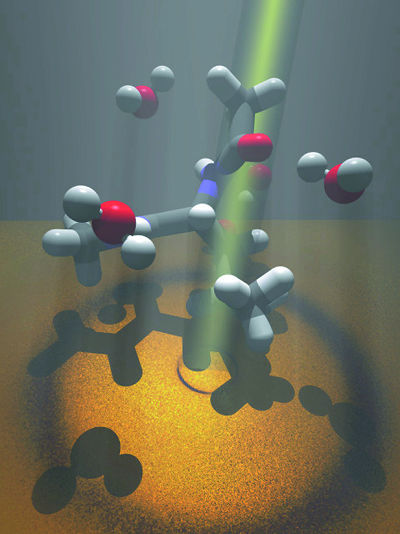 LBL
LBL
An
impressionistic illustration showing x-rays or neutrons
being shone through leucine (the gray and white structures)
dissolved in water (the red and white structures).
|
The Garden
of Converging Paths
One way to test
ideas about how proteins fold is to start with a shape smaller and
less intricate than most proteins, made from units less complicated
than amino acids. Supercomputers simulate the behavior of model
polymers, which in their native structure-analogous to the thermodynamically
stable conformation of a fully folded protein-resemble jungle gyms
made from Tinker-Toy-like sticks and balls.
Instead of the
varying angles between amino-acid residues in a real protein, the
stick-and-ball units, or mers, in a lattice model bond to their
neighborsonly at right angles or straight ahead; instead of a real
amino acid's complex of properties, a mer can be assigned just a
few.
"Lattice models
aren't meant to model specific proteins," says Rokhsar, "but they
give a good representation of certain aspects of real processes
in manageable time." Using the Cray T3E at the National Energy Research
Scientific Computing Center (nersc), Rokhsar and Vijay Pande, an
assistant professor of chemistry at Stanford University, discovered
unsuspected regularities in the folding pathways of model polymers.
When the simulated
temperature was raised high enough, their lattice model unfolded
completely; when the temperature was lowered, the model refolded,
writhing through almost a million different positions before settling
into its native, low-energy structure. Even with a 48-mer model-roughly
equivalent to a small protein-the possible initial conformations
are astronomical, and each path to stability is potentially unique.
To see how different
properties of the components may affect transition states and pathways,
Rokhsar, Pande, and graduate student Nicholas Putnam designed three
other small, 27-unit polymers with the same native-state conformation,
based on three widely used types of lattice models.
In the simplest
version, only mers that touched in the native state attracted each
other-all others were energetically neutral. A more complex model
had three kinds of mers in competition, with like types attracting
one another more strongly than unlike types. The most complicated
lattice model used mers with 20 discrete values derived from those
of real amino-acid residues.
"In the two
simpler cases, we found that folding pathways could pass through
just two distinct core transition states," says Rokhsar. "The more
complex model had only a single transition state. Both these behaviors
are observed in the folding of some small natural protein structures."
Knowing more
about the transitional structures that a folding protein must pass
through sheds light on which positions in the chain of amino-acid
residues are most critical for a flawless fold-those positions where
mutations that substitute one amino acid for another are likely
to have the greatest effect on a protein's shape, for better or
worse.
Water, Water,
Everywhere
Proteins don't
exist as ideal Platonic forms; their real environment consists mostly
of a warm solvent, namely water. By combining theoretical and computational
approaches, such as lattice models, with data from experiments,
physical chemist Teresa Head-Gordon of the Physical Biosciences
Division and her colleagues have detailed water's essential role
in driving protein folding and stabilization.
One important
measure of amino acids is their varying degrees of hydrophobicity,
or "fear of water." Oil is hydrophobic-that's why oil drops remain
separate in water-while hydrophilic ("water-loving") substances
readily dissolve in it. Many proteins have a hydrophobic core and
a hydrophilic surface.
By measuring
the intensities of x-rays or neutrons scattered by water molecules
alone - and then by leucine molecules dissolved in water-Head-Gordon
and her colleagues were able to analyze the structure of water near
the leucine. They conjectured that these water structures, much
more highly ordered than water in bulk, give rise to forces that
differ among different kinds of amino acids and thus influence folding
pathways.
When Head-Gordon
and her colleagues applied what they had learned from scattering
experiments to lattice models of polymers, they found that by including
accurate solvation forces they could go a long way toward making
the models more realistic mimics of actual proteins. Some models
were swiftly eliminated, and the performance of others was improved
to exhibit faster folding and more cooperative folding transitions.
In addition to a basic understanding of the folding of all proteins,
such studies may lead to specific insight into classic sequences
such as the "leucine zipper" that joins secondary protein structures
into dimers through hydrophobic attraction-a sequence that, when
mutated, may play a prominent role in activating cancer-causing
genes.
SCOPing Out
Folds
 LBL
LBL
An
illustration of the advanced state of computational modelling
|
Simple theoretical
models bolstered by experimental data are one approach to faster
protein-structure prediction. Another way to use computers to translate
dna sequences into protein structures is to work directly from a
growing library of known folds.
Describing her
method of predicting the folds of unknown proteins, Dubchak explains
that "traditional methods compare unknown gene sequences to known
protein sequences or structures residue by residue, searching for
correspondences. But what happens when no similar sequence exists?
I decided to tackle the problem differently, from a taxonometric
perspective."
Dubchak assessed
the physical properties of each of the 20 amino acids found in proteins-such
characteristics as hydrophobicity, polarity, van der Waals radius
(size), and the like-and reduced these to a number of vectors representing
the residue's cooperative influence on a fold.
Taken together,
the vectors of an unknown sequence do not specify an exact shape
so much as they suggest one that may or may not resemble a fold
already included in the Structural Classification of Proteins (scop),
a library of experimentally observed folds developed by the Medical
Research Council's Laboratory of Molecular Biology in Cambridge,
England.
Dubchak "trains"
neural networks, built with computer processors, to recognize sequences
that produce scop-like folds; at present, about a fourth of new
sequences can be matched confidently to folds already in the library.
Those that don't match known shapes represent folds that have not
yet been discovered (or they signal that the neural network doesn't
have enough information or hasn't yet learned to recognize the relationship).
Armed with the
knowledge that the fold of a new protein resembles familiar folds,
biologists can hypothesize the new protein's evolutionary relationships
and biological functions, as well as how it may bind to other proteins
and to specific chemicals, including drugs.
However, because
entirely different dna sequences may produce structures of similar
topology, large uncertainties remain. For example, the resolution
of a neural-network fold prediction may be limited to several times
the typical distance between atoms-and two structures possessing
the same fold may be significantly different in size.
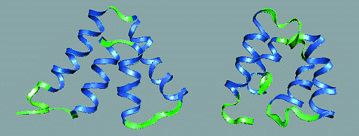
LBL
Using
global optimization programs such as GOSPEL, small protein
structures can be predicted.
|
Teresa Head-Gordon
seeks to reduce these uncertainties by invoking the gospel-that
is, "global optimization strategies to probe energy landscapes."
Head-Gordon's goal is to find, within the range of possibilities,
the protein structure corresponding to a specific sequence that
has the lowest energy.
Neural-network
predictions such as Dubchak's supply "soft constraints" on shape
and specify known secondary structures such as alpha helices and
beta sheets. By applying gospel - using force-field models such
as amber and charmm, and descriptions of aqueous solvation learned
from theory and experiment-vaguely defined "coil" structures, which
are more challenging, can also be resolved.
In the course
of comparing candidates, the algorithm applies these empirically
derived functions to areas of the fold accessible to water; it imposes
an extra energy penalty on structures with exposed hydrophobic surfaces.
Repeated perturbations of amino-acid positions use gospel to lower
the energy further, homing in on the lowest possible total energy.
Global optimization
is a voracious consumer of computer power and time. Using the Cray
T3E-900 at nersc, Head-Gordon and her colleagues have tested their
algorithm against simple "target" proteins. In the case of 1pou,
for example, a dna binding protein with 72 amino acids arranged
as several alpha helices, the structure predicted by gospel from
sequence gave a reasonable estimate of the fold but had some six
percent higher binding energy than the known structure derived from
nuclear magnetic resonance imaging.
"We have still
not reached crystal structure energy yet, so further improvements
in structure are still possible!" Head-Gordon exclaims.
Nevertheless,
while improvements in the underlying model are needed, global-optimization
results have been sufficiently encouraging to attempt larger proteins
with more complex structures, including pure beta sheets and mixed
alpha-helix, beta-sheet proteins.
Bundles and
Beads and Barrels and Saddles

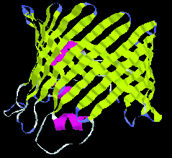
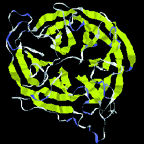
LBL
Protein
shapes reveal recurring structural motifs called "folds" that
help define physical and chemical properties.
|
Proteins are
like strings of beads wound into bundles. Their structure is described
at increasingly intricate levels. Primary structure is a chain of
amino-acid residues, chemical units linked to their neighbors by
peptide bonds, like snap-together plastic beads. The 20 amino acids
that can form proteins differ in size, shape, electric charge and
polarity (which affects interaction with water), hydrophobicity
("oiliness"), and other properties. Researchers have assigned single-letter
designations to each, from A for alanine through Y for tyrosine;
thus primary structure, the polypeptide chain, is given by a string
of letters, e.g., MEIMKKQNSQINEINKDEIFV. . . .
Secondary structure
results from the angles between amino acids, plus the hydrogen bonds
that may form from one residue to another. Repeating bonds and angles
commonly form alpha helices and beta sheets (or sometimes variations
of these) and their hairpin or crossover connections-plus a variety
of turns, which often expose active chemical groups on the protein
surface, and a few other structures such as loops and "paperclips."
Tertiary structures
are made from helices, sheets, and other secondary elements. A particular
configuration of these is called a fold. There are roughly 500 known
folds, a dozen of which occur very commonly, some with names like
"barrel" or "sandwich" or "saddle"-out of some 6,000 to 10,000 predicted
to exist. Remarkably, many proteins that have completely different
sequences of amino acids are structurally identical-a strong hint
that this structure has inherent evolutionary advantage.
While a protein
may consist of a single polypeptide strand incorporating a particular
fold, others are built from separate strands. A famous example of
quaternary structure is hemoglobin, which combines two pairs of
identically folded chains in a single molecule capable of snapping
up, carrying, and releasing oxygen in the bloodstream and tissues
of the human body.
In vivo,
In vitro, In silico
Models that
derive values from real amino-acid residues and realistic watery
environments can help us understand the folding of real proteins,
and the shapes and functions of many unknown proteins can be deduced
from libraries of known folds. These and yet more sophisticated
and powerful computer techniques are essential, for a functioning
protein is dynamic, while the protein structures determined by crystallography
are static-and even at the present rapid experimental clip it could
take another century to decipher the full atomic structures of all
the proteins in cells by experiment alone.
Daniel Rokhsar
and his colleagues have also studied the molecular dynamics of a
real protein structure, not under natural conditions or in an experimental
set-up, but in silico, using a fully realistic "all-atom" computer
model in which the properties of every atom in every amino acid
are represented, and thousands of water molecules are explicitly
treated.
"Even in long
runs on powerful computers, with all-atom calculations it's only
practical to model a few nanoseconds of real time," says Rokhsar,
"yet real proteins typically fold up in a few milliseconds"-a million
times longer. "So we modeled a very small part of a real protein,
a common structure called a beta hairpin. Instead of trying to watch
it fold up, we watch it unfold, which at the high temperatures of
the simulation is a much quicker process."
Unfolding occurs
in a series of discrete steps which always happen in the same order.
Each represents the dissolution of a specific part of the hairpin
structure, recalling the transition states of lattice models.
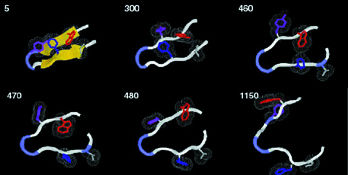 LBL
LBL
At
400 degrees Kelvin, a protein's beta hairpin, 16 amino-acid
residues long, starts to unfold. The time to each step of
this all-atom simulation is shown in trillionths of a second.
|
Much faster
and more manageable supercomputers will be needed to study larger
protein structures at the atomic level. The largest yet studied
in silico, with 36 residues and 12,000 atoms, was tracked over the
course of a single microsecond by researchers at the University
of California at San Francisco; the simulation took a Cray T3D and
a Cray T3E-600 running for two months each, and the model did not
reach the real protein's native conformation.
To rationally
design drugs that can attack specific disease mechanisms, to create
novel industrial enzymes, to engineer new organisms that can increase
food production, clean up waste, and restore the environment-these
potential benefits all depend upon accurate, intimate knowledge
of a wide range of protein structures and their possible mutations.
Every scrap of experimental knowledge, every advance in calculating
the molecular dynamics of model proteins, all are essential to the
solution of the protein folding problem, a goal that still glimmers
in the future.
|
