Extreme Maths: Infinity - The Art of the Infinite

The true mysteries of mathematics lie at the limits of our thinking - infinity. Reach beyond what you think is possible and you start to explore the wonders of maths at the extremes.

When you look down the tracks you won't see a train, since these days the trains never seem to be running - but you will see infinity. Follow that point where the tracks meet - it must be no more than a mile away; but when you get there, where has it gone? Vanished again.

The Renaissance painters made sense of pictorial space by organising it around this vanishing point. That wonderful Florentine, Leon Battista Alberti, described how he translated three dimensions into two: "I make a veil, loosely woven of fine thread, dyed whatever colour you please, divided up by thicker threads into as many parallel squares as you like, and stretched on a frame. I set this up between the eye and the object to be represented, so that the visual pyramid passes through the loose weave of the veil."

One-point perspective gave rise in time to two vanishing points – but can you picture a space with an endless number of points at infinity – one for each point on the horizon? It takes outrageous imagination and an Art of Extremes to do this - and that is exactly what mathematics is. Just as heard melodies are sweet but those unheard are sweeter still, so what the eye can be trained to see is marvellous - but the mind's eye sees wonders incomparably greater.

A painting, a piece of sculpture, a work of architecture are organised above all by gracefully balanced masses - and again the infinite in mathematics lies in the hidden, central room of this art of proportion. Which rectangle has the most pleasing ratio of length to width, for example? Experiment for yourself by making a rigid frame with a sliding fourth side, and test where your friends think best to halt it. Was the ratio of width to length close to 2 x 3, 3 x 5, 5 x 8 - the standard sizes of index cards and photos? Or to some other pair of adjacent numbers in the sequence:

Leonardo of Pisa, nicknamed Fibonacci, was an Italian mathematician at the start of the thirteenth century, who showed how to form this elegant sequence of numbers, which is linked to our understanding of what makes pleasing proportions. Have you discovered how to make new terms of his sequence? The 'secret' is to add the previous two. But why should that sequence have anything to do with pleasing proportions?

The great Piero della Francesca wrote a book, "On the Divine Proportion", and in his paintings framed their parts and the whole in rectangles with these ratios. Leonardo da Vinci saw that tree branches, as they spiral up the trunk, are spaced in these proportions too. Virtually all artists work on these principles, whether they realize it or not. Pine cones and nautilus shells, antlers, the crossing rows on a sunflower's head - again and again these Fibonacci ratios appear in nature. But it is only in mathematics, the art of the infinite, that these ratios are carried beyond the visible to their invisible extreme: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8 and so on approach a certain number, called The Golden Mean (roughly 1.618...): which describes the ideal proportion that the finite ratios in art and nature only approximate.

Is this ideal divine or diabolic? The star-shaped pentagram, sign of the Black Arts and trap for Mephistopheles, is made up of segments in just this golden ratio. And is it angels of light or of darkness who stand behind the mathematician in his daring leap into the infinite? One answer would be to look at Escher's self-portrait, surrounded by his mannerist art with its staircases that both ascend and descend, inside-out reflections, space tiled with birds seen one way, fish the other – all planned with the most cunning mathematics.

with thanks to Professor Christopher Leaver

Sunflowers

But Escher no more stands for all of modern art than Parmigianino stands for all of classical art. Art and mathematics, are both dependent on balance, and balance in mathematics is stored in what most people find frightening: equations. Yet what is there to be frightened about? These expressions, pivoting on the slender fulcrum of an equals sign, are just different ways of seeing the same thing; equations are the Cubism of mathematics: here is this profile, here is this face seen front on – and they are the same!

Take for example the five Platonic Solids: those polyhedra from pyramid through cube to icosahedron, whose nested totality Kepler saw as emblematic of the universe. You find them everywhere in nature and art: the building-blocks of space. How different they are from one another - yet a most remarkable equation relates them all. Just count the number of corners (vertices, to give them their technical name) on any one of them - call the result V. Now add up the number of edges and call it E, and the number of faces, F. What do you find?

Not much in common here. Find V, E, and F for the octahedron, dodecahedron, and icosahedron as well - a bunch of numbers. Yet in every case, V - E + F = 2!

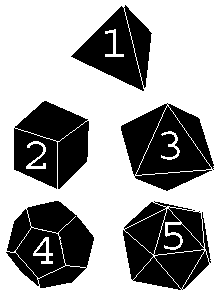
The Five Regular Polyhedra or Platonic Solids

1 - Tetrahedron/Pyramid
2 - Cube
3 - Octahedron
4 - Dodecahedron
5 - Icosahedron

How wonderful! Mathematics ferrets out what is universally true in the infinite scatter of seemingly haphazard phenomena, and expresses it in eternal equations. This art of the infinite lies behind all of our arts (think of music, whose harmonies are the audible expression of ratios), but it then goes beyond them.

"I sent my soul through the invisible," wrote the eleventh century Persian mathematician and poet Omar Khayyam. Let's take only one excursion to illustrate this. That cube we just spoke of had 8 vertices, 12 edges, and 6 faces. What can we say about four-dimensional cubes? What can we say at all about four dimensions? Astonishingly enough, we can say a lot. We can't see a four-dimensional cube, but we can think it, and it has16 vertices, 32 edges, and 24 faces! Shall we go on? A seven-dimensional cube has 672 faces. A ten-dimensional cube has 5,120 edges. We could go on...

We could go on, because the true home of mathematics is at the limit of all our thinking. Calculus, that wonderful invention of Newton (and independently, of the German diplomat, philosopher, and mathematician, Gottfried Leibniz), comes to grips with change as Seurat and the Impressionists did, by reducing reality to flickering points, and then rebuilding the world more profoundly.

Artist’s live flamboyant lives, mathematicians tend to be thought of as reclusive and dry. How could they possibly be of the same breed? Mathematicians come in all the usual flavours: some are playful, some arrogant, some devious, and others direct. John Maynard Keynes pictured Newton as the last of the Magi, trying to wrest its secrets from the universe alone in his tower at night. Da Vinci - half artist, half mathematician - comes down to us as ambiguous as his Mona Lisa's smile.

Stare into the maelstrom...

Like the structures they probe for, what is essential to mathematicians often lies concealed - for not only does nature hide itself, as Heraclitus said long ago, but it is art to hide art. And it is the infinite that lies hidden in the least grain of sand.